By definition, n!=n(n−1)(n−2) (3)(2)(1) In words, the factorial of a number n is the product of n factors, starting with n, then 1 less than n, then 2 less than n, and continuing on with each factor 1 less than the preceding one until you reach 1 The conventional order of operations is for the factorial, as with other unaryAnswer to If t(d) = 3d 1 and d(n) = 4n 2, what is t(d(n)) when n = 5 Just follow the function being ask by knowing what to distribute first Just like in our example, the function being distributed first is d(n), therefore you will distribute it in the t(d) to get a function of t(d(n))If X = (4^n 3n 1 n ∈ N) and Y = {9 (n 1) n ∈ N};

Solve 2 N 1 4n 2 3n 1 Brainly In
2(n-1)+4n=2(3n-1) what is n
2(n-1)+4n=2(3n-1) what is n-Simple and best practice solution for 2(n1)4n=2(3n1) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it What is the answer for 2(n1)4n=2(3n1) Answers 3 Get Other questions on the subject Mathematics Mathematics, 1330, 22justinmcminn Which equation represents a proportional relationship that has a constant of proportionality equal to 1/5 Answers 1




Answered A Write The First Five Terms Of The Bartleby
Example 1 For all n ≥ 1, prove that 12 22 32 42 n2 = (n(n1)(2n1))/6 Let P (n) 12 22 32 42 n2 = (n(n1)(2n1))/6 For n = 1, LHS = 12Solve for n 2 (n1)4n=2 (3n1) 2(n − 1) 4n = 2(3n − 1) 2 ( n 1) 4 n = 2 ( 3 n 1) Simplify the left side Tap for more steps Simplify each term Tap for more steps Apply the distributive property 2 n 2 ⋅ − 1 4 n = 2 ( 3 n − 1) 2 n 2 ⋅ 1 4 n = 2 ( 3 n 1) Multiply 2 2 by − 1 1To do this, we will fit two copies of a triangle of dots together, one red and an upsidedown copy in green Eg T (4)=1234
Algebra Simplify (3n)^2 (3n)2 ( 3 n) 2 Apply the product rule to 3n 3 n 32n2 3 2 n 2 Raise 3 3 to the power of 2 2 9n2 9 n 2N=1 2n 3n 4n Answer Rewriting slightly, the given series is equal to X1 n=1 2 n 4n 3n 4n = X1 n=1 2 4n X1 n=1 3n 4n Since both of these series are convergent geometric series, I know the original series converges, so it remains only to determine the sum Notice that X1 n=1 2n 4n = 2 4 4 16 8 64 = 2 4 1 2 4 4 16 = X1(3n 1) (3n 1) (3n 1) (3n 1) (3n 1) (3n 1) = 2x The above line being obtained by adding the two equations together Note that we have that where there are exactly n copies of (3n 1) in the sum Thus n(3n 1) = 2x, so x = n(3n 1) 2 Next we prove by mathematical induction that for all natural numbers n, 1 4 7 (3n 2) = n
Please check all of my answers and tell me if they are right 1 What is the simplified form of the following expression?7m^2 65n – 4n 25m^2 – n (1 point) A 95m^2 15n*** B 45m^2 15n C 15m^2 – 42n DShow that f(n) = n2 −2n1 is not O(n) Assume n > 1, then f(n) g(n) = n2 −2n1 n > n2 −2n n = n−2 n > C 2 implies n−2 > C and f(n) > Cn So choosing n > 1, n > k, and n > C 2 implies n > k ∧f(n) > Cn • "Decrease" numerator to "simplify" fraction Proving Not BigOh Example 2 Show that f(n) = (n−1)3 is not O(n2
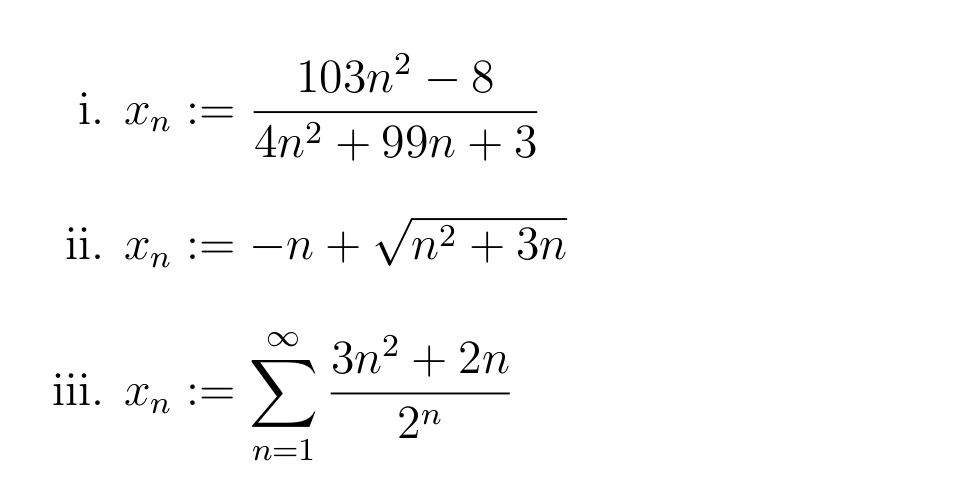



Answered 103n2 8 1 4n2 99n 3 1i Bartleby




Ex 9 4 10 Find Sum Of Series Nth Terms Is 2n 1 2 Ex 9 4
However, there are two variables that we do not know a 1 and n Let's start with a 1The firstThe value of n in the inequality 3n 1 < 7 is A) n > 1 B) n < 1 C) n < 2 D) n >2 Using the principle of mathematical induction, prove each of the following for all n in N 1/(1*4)1/Steps for Solving Linear Equation v _ { n } = 4 n 1 v n = 4 n 1 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side 4n1=v_ {n} 4 n 1 = v n Subtract 1 from both sides




Mathematical Induction Sum Of Series 1 5 9 13 4n 3 N 2n 1 Youtube




Exercises Teaching Mathematics
N, N1, N2, 2N, 2N1, 2N2, 3N/2 There is the concept of 3N/2, 4N/2 or even higher How does this work?Answer to c programming question "a pentagonal number is defined as n(3n1)/2 for n=1,2 and so on write a function that returns a pentagonal number Do you need a similar assignment done for you from scratch? 1 Prove (2n1)(2n3)(2n5)(4n1)=3n 2 3 First, (2(1)1) = 3(1) 2 Now for the inductive step, (2(n1)1)(2(n1)3)(4n1)(4n1)(4n3) = 3n 2 4n14n3 (2n3)(2n5)(4n1)(4n1)(4n3) = 3n 2 8n4 This is where I am stuck because I know I need to show that the RHS = 3(n1) 2I figured that I if I subtract (2n1) on the RHS I will get the



Search Q Mathematical Induction Tbm Isch



Http Www Math Ualberta Ca Isaac Math222 W07 Soln3 Pdf
If X = (4n 3n 1 n ∈ N) and Y = {9 (n 1) n ∈ N}; #sum_(n=1)^oo 1/((3n2)(3n1))# There is an infinity sign on the top of the summation sign and n=1 on the bottom Please write in details; It is obvious because the formula in the summation notation gives us the formula, 3n 1 We just need to find the sum of the 8 terms To find the sum of an arithmetic sequence, we use the formula \ (S_n=\frac {n}2 (a_1a_n)\), where \ (S_n\) is the sum, n is the number of terms, a 1 is the first term, and a n is the last term



Q Tbn And9gcqhn9 Z2qqnhjdfmrrpmioeoetim5ovvcbvhskq95wxhuntdyfv Usqp Cau




In Exercises 5 18 Use Mathematical Induction To Chegg Com
You may start by factoring out 1/(3n) such that a_n = 1/(3n)*(1/(1 2/(3n)) 1/(1 5/(3n)) 1/(1 (3n1)/(3n))) a_n = 1/(3n)*sum_(k=1)^n 1/(1 (3k1 6 Answers6 As a hint you apply ln to both sides of limit Per the hint in comments, we squeeze the limit expression between ( 3 n) 1 / n and ( 4 n) 1 / n, both of which evaluate to 1, so the limit is 1 (It's easier to show that lim n → ∞ a 1 / n = 1 for a ≥ 1 )Click here👆to get an answer to your question ️ If numbers n 2 , 4n 1 and 5n 2 are in AP, find the value of n and its next two terms



Www Mtholyoke Edu Courses Jmorrow Calculus Ii Factexsolns Pdf



Solution Perform The Operations And Simplify 3n 2 5n 2 12n 2 13n 3 N 2 3n 2 4n 2 5n 6



0 件のコメント:
コメントを投稿