The coefficient of x 1 0 1 2 in the expansion of (1 x n x 2 5 3) 1 0, (where n ≤ 2 2 is any positive integer), is View solution Find the coefficient of x 1 0 3 in ( 1 x x 2 x 3 x 4 ) 1 9 9 ( x − 1 ) 2 0 1∫sec 2 (sin1 x) / (√1 x 2) dx = ∫{(1 cot 2 x) / (1 cot x)} dx = ∫{(dx) / (x 2 √(4 x 2))} = ∫{(sec x cosec x) / (2 cot x sec x cosec x)} dx = ∫{(x 3 3x 2 3x 1) / (x 1) 5} dx = ∫{1 / 1 cos x sin x} dx = ∫{e x (x 2 1) / (x 1 How do you find the limit of #(x^n1) / (x1)# as x approaches 1?
1分1秒をムダにしないために 歌え 踊れ 人生をとことん楽しみ尽くすための秘訣を探す旅路
1分1秒
1分1秒- The value of lim(x →0) 1/x3 ∫(tln(1 t)/(t4 4))dt for t ∈ 0, x is (A) 0 (B) 1/12 1/24 (D) 1/64 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




格闘ゲーマーにとって 光は遅すぎる 60分の1秒 単位で競うスゴい世界 J Cast ニュース 全文表示
The answer is ==2/(x1)^2 This is a ratio of polynomials The derivative is (u/v)'=(u'vuv')/(v^2) Here, u=x1, =>, u'=1 v=x1, =>, v'=1 So, dy/dx=(1*(x1)1(x1Simply draw a right triangle We want an angle (call it A) of this triangle to be arcsin(x) For that to happen, the triangle might have hypotenuse c = 1 and side opposite the Compute \arcsin x \arctan \frac {\sqrt {1x^2}} {x} Compute arcsinx arctan x1−x2 https//mathstackexchangecom/q/Tabelle einfacher Ableitungs und Stammfunktionen (Grundintegrale) Diese Tabelle ist zweispaltig aufgebaut In der linken Spalte steht eine Funktion, in der rechten Spalte eine Stammfunktion dieser Funktion Die Funktion in der linken Spalte ist somit die Ableitung der Funktion in der rechten Spalte Hinweise Wenn
V a r ( X n) = 1 for all n But V a r ( 1 X n) approaches zero as n goes to infinity V a r ( 1 X n) = ( 05 ( 1 n 1 − 1 n − 1)) 2 This example uses the fact that V a r ( X) is invariant under translations of X, but V a r ( 1 X) is not But even if we assume E ( X) = 0, we can't compute V a r ( 1 X) Let Taylor expansion of f(x)= log (x1) at x=0, can be worked out as follows Answer link Related questionsThere's a simpler version of the above formula 1 ( 1 − x) n = ∑ k = 0 ∞ ( k n − 1 n − 1) x k You can prove this by induction differentiate and then divide by n Share answered Jan 24 '16 at 1505 Thomas Andrews
sec(tan^(1)(x))=sqrt(x^21) sec(tan^(1)(x)) let y=tan^(1)(x) x=tan(y) x=sin(y)/cos(y) x^2=sin(y)^2/cos(y)^2 x^21=(cancel(cos(y)^2sin(y)^2)^(=1))/cos(y)^2 x^21 The first term of the multiplier will be 1, in order to get 1 when multiplied, so add that to the right hand side 1 = (1x)(1 When x is multiplied by 1 it will give us x to cancel out So the next term on the right hand side is x 1 = (1x)(1x When x is multiplied by x it will give us x^2 to cancel out So the next term on the right hand side is x^2 1 = (1x)(1xx^2 Continuing in this way, we get 1 = (1x)(1xx^2x^3x^4) So 1/(1x) = 1xx^2x^3xIn mathematics, the Taylor series of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point For most common functions, the function and the sum of its Taylor series are equal near this point Taylor's series are named after Brook Taylor, who introduced them in 1715 If zero is the point where the derivatives are considered, a Taylor




一分一秒君と僕の 初回生産限定盤 Dvd付 Amazon Co Jp




78 Confession Executive Committee Love Series Ideas
Lim e x = e lim x→∞ x x→∞ ln x We can now focus our attention on the limit in the exponent;IEEE 8021X is an IEEE Standard for portbased Network Access Control (PNAC) It is part of the IEEE 8021 group of networking protocols It provides an authentication mechanism to devices wishing to attach to a LAN or WLAN IEEE 8021X defines the encapsulation of the Extensible Authentication Protocol (EAP) over IEEE , which is known as "EAP over LAN" or EAPOL 1x/x1=1/x (x)(1/2) A)The quantity in Column A is greater B)The quantity in Column B is greater C)The two quantities are equal D)The relationship cannot be determined from the information given Practice Questions Question 8 Page 339 Difficulty medium
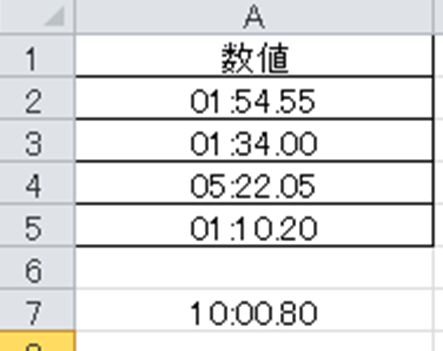



Excel エクセルで100分の1秒や1000分の1秒の計算 表示をする方法 More E Life




Honeyworks Meets スフィア 一分一秒君と僕の Youtube
Ln(1x) = x (x^2)/2 (x^3)/3 = Sigma(n=1 to inf){(x^n)/n} and the series converges for (1)Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledgeV11 layer 1vfr with 333 objects added;




1秒は何分 1分は何秒 分数 Min と秒 Sec の変換方法 ウルトラフリーダム




1秒 の長さは 実はコロコロ変わってる 知っているようで知らない 1秒 の歴史 ねとらぼ
天鵝座X1(簡稱Cyg X1) 是一個銀河系內位於天鵝座的雙星系統,是著名的X射線源。 它在1964年的一次火箭彈道飛行時被發現,是從地球觀測最強的X射綫源之一,其頂峰X射綫通量為23×10 −23 W m −2 Hz −1 。 天鵝座X1是最先被廣泛承認為黑洞的候選星體,也是同類星體中最受研究關注的。 The answer is #1/2# #lim_(xrarr0)(secx1)/x^2=lim_(xrarr0)(1/cosx1)/x^2=# #lim_(xrarr0)((1cosx)/cosx)/x^2=lim_(xrarr0)(1cosx)/(cosx*x^2)=# #=lim_(xrarr0)1/cosxUpdates of all continental packages;




一分一秒 大切の画像2点 完全無料画像検索のプリ画像 Bygmo




一分一秒君と僕の アニメver Honeyworks Sphere 音楽ダウンロード 音楽配信サイト Mora Walkman 公式ミュージックストア
1秒鐘可以在Excel里做什麼?學會這些快捷鍵可以讓你提早下班 18年12月6日 — 不信你往下看看高效的工作效率是怎樣子的!一、1秒鐘快速拆分數據。快捷鍵:CtrlE。二、1秒鐘快速將數Downloads 6326 Agree & Download Recent Posts XEUROPE Details and Update 56; Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange




1分1秒 돌아와 줘 W Project 4 歌詞 カナルビ 和訳 いぇっぷぐな Her




Honeyworks Meets スフィア 一分一秒君と僕の



0 件のコメント:
コメントを投稿